On 4 September 2016 I gave a condensed version of this essay as a talk to the Philosophy Forum in Melbourne, Australia.
The Nature and Existence of Time
The present time “does not exist.”
It isn’t even fleeting.
The past is gone and often missed,
And just keeps on retreating.
They say tomorrow never comes –
You can’t give it your greeting.
The message of this simple rhyme
Seems very, very strange,
For if there’s no such thing as time,
Then what could ever change?
(GL 2013)
We all are aware of something called time, but it is hard to define what it is. It seems to have something to do with change, or with sequences of events, but we are still aware of it when nothing seems to be happening. And we have concepts of now, and before and after, which seem to be essential aspects of time.
But what is time? Is there such a thing as the present time? Does time exist? What do philosophers and scientists think about it?
There are more philosophical opinions on this topic than there are on most other parts of the physical sciences. And scientists also disagree about some aspects of time. So this essay will be just a simple overview. And there is much more to say about time than is covered here.
Subjectively, the time is always “now”. But “now” is always changing. There is a point of view that, while time is something that we are conscious of, by the time we become conscious of the present time it has already gone, so the present time does not exist. There is a similar argument that the present time can have no duration whatsoever. But quantum theory does not allow anything as precise as absolutely nothing, so the present time exists for an extremely short but undefinable period of time. There is an argument that, while the present time exists, the past and the future do not. This point of view is called Presentism.
We have the feeling of time passing, sometimes seemingly passing quickly, sometimes seemingly passing slowly. And the time that went quickly for one person might, at the same time, have gone slowly for someone else. So, subjective concepts of time can seem contradictory, or a bit quirky. There are various timekeeping processes in the human brain, and the cognitive areas of the brain deal with a huge range of matters including time and emotions. This allows feelings about the length of elapsed times to be affected by emotional, spatial and other contexts.
We might think that science is much more constant in its dealings with time. Scientists make many precise measurements of time relating to many kinds of physical phenomena, all of which produce consistent results. Scientists can predict and control such things as the flight of space ships that perform intricate manoeuvres on and around distant planets where precise timing is critical. But, in doing so, they have to take account of some tricky and apparently illogical things that relate to the theory of relativity.
Relativity
There are actually two theories of relativity. The special theory of relativity explains how, when an object is moving, an observer measuring a phenomenon on that object will find, among other things, that the elapsed time associated with the phenomenon “lengthens”, or “slows down”. That is, to the observer, everything that happens on the distant object takes longer than if it had occurred at the observer’s own location. However, for someone on the moving object, time has not slowed down, but it does appear to have slowed down at the first observer’s location. This is because the observers on each object would regard their own location to be stationary and the other to be the one that is moving.
This effect becomes greater as the speed of the object increases. The amount of lengthening can be calculated by a mathematical formula known as the Lorenz transformation, which is:
tv = t0 C /(C2 – v2)–2
where tv is the elapsed time of the observed phenomenon on the moving object,
t0 is the measure of elapsed time at the object’s location,
v is the speed of the moving object
and C is the speed of light.
This Lorenz transformation applies also to a similar increase of the mass of observed moving objects. An inverse Lorenz transformation applies to length, which shortens.
The special theory of relativity is based on two assumptions:
- the laws of physics will appear to be the same irrespective of how near or far a particular phenomenon occurs from where the observed measurements are made, including when whatever is being observed and measured is moving relative to the observer; and
- the speed of light in a vacuum has a constant value.
The general theory of relativity explains how time slows down under the force of gravity, and this effect depends on how great the force is at the particular location. The stronger the gravitational force at that location, the more slowly time passes there. A gravitational force is caused by the mass of some object. It is stronger with objects of larger mass, and it becomes weaker in proportion to the square of the distance from the object. Strictly speaking, the distance is measured from the centre of the object. So, if you are standing on an object such as the earth, the relevant distance is measured from the centre of the earth. And this means it is slightly different at different places around the globe.
So a clock will run more slowly at sea level than if it was on a geostationary satellite (one that stayed over the same point on Earth), because the force of gravity is greater at sea level, which is closer to the centre of the earth.
(The strength of the gravitational force between two objects is calculated by the formula:
F = G*m1*m2/d2
Where:
* is a multiplication sign
F is the attractive force between the objects
G is the universal gravitational constant,
m1 and m2 are the masses of the two objects
and d is the distance between the centres of mass of the two objects.
This force is attracting both of the objects equally.)
(Actually, the essence of general relativity is that there is no gravitational field as such. What appears to be a gravitational field is the distortion of the otherwise “straight” space-time, which is caused by the mass of each object. But the effect is the same irrespective of which way you think about it. Another example of having an apparent and a more rigorous depiction of a physical process is what we call centrifugal force, which is not a force but a consequence of Newton’s first law of motion.)
The concept of space-time, which is an essential part of the special theory of relativity, implies that, if there no such thing as time, there would be no such thing as space-time or even space.
The general theory is based on the assumption that the attributed gravitational force exerted by an object is identical with the inertia of that object, that is, with the force required to change the motion or the condition of rest of the object.
The accuracy of both theories has been confirmed from measurements of natural phenomena and also from specially designed experiments.
These theories need to be taken into account in designing such things as global positioning systems and the operation of space missions. So these effects are not just subjective.
Despite this, some physicists think that time does not exist because, they say, the theory of quantum gravity does not require the concept of time. The theory of quantum gravity was developed in an attempt to describe gravity in quantum terms, and so resolve one of the problems arising from the fact that Einstein’s theory of gravity is not compatible with quantum theory. But the incompatibilities remain, and quantum gravity has intrinsic inconsistencies. But, even if it were to be made consistent, and accurate in its descriptions of the relevant phenomena, it is only one part of fundamental physics. Time is relevant to all other aspects of physics. It is an essential component of the concepts of velocity, acceleration, force and energy. If none of these things existed, there just might still be matter and space, but they could have no characteristics except their location, and nothing could happen.
The theory of relativity regards the universe to be continuous, that is, every piece of matter and energy and space and time can be divided into smaller and smaller parts infinitely. Quantum mechanics regards all of these pieces to be “lumpy”, that is, there is a limit to how small each piece can become.
One attempt to unite the theory of relativity with quantum mechanics is the theory of loop quantum gravity. This theory postulates that the fundamental components of the universe are interlocking vibrating loops, each of which is very much smaller than a proton or an electron. The many different contortions and vibrations of these loops incorporate all the possible conditions of all the things that the present “standard” theory regards to be fundamental. The universe is the sum total of all the loops, and the loops make the universe lumpy. As some physicists point out, this structure does not include time as such. But the strings are vibrating, that is their conditions are continually changing, which inherently comprises time.
The only way I can interpret loop quantum gravity is that this kind of universe must consist of loops that embody every tiny fundamental piece of the universe in all of their different conditions from what we might think of as the beginning of time to the end of time – a bit like the block universe, which I will describe later in this essay.
So, while loop quantum gravity does not explicitly refer to time as such, it may still do so implicitly. Similarly, our common concept of the “force” of gravity might be regarded as being implicit in the general theory of relativity.
Calculations using the concept of a force of gravity, and also those using the concept of time, produce results that are consistent with our observations of how the universe works. Is this just good luck? It might be for gravity. But no matter which model you have for the universe, from the block universe to the others derived from it, to loop quantum gravity, and to the concept of space-time, there is the curious occurrence of one particular component whose interactions and relationships are always unidirectional. This means that this component is not symmetrical in a way that all the others are. We call this component – or, perhaps, this relationship – time.
Symmetries
Many scientists have feeling (or perhaps an aesthetic assumption) that all the laws of science should be symmetrical.
This may be because the concept of symmetry has been useful in helping physicists and mathematicians to develop ideas about the underlying processes of the universe. Symmetry is a characteristic of certain things and processes. We are all familiar with symmetrical shapes that look exactly the same when turned upside down or reflected in a mirror. For a thing or a process to be symmetrical, it must continue to appear the same, or to act in the same fashion, after being manipulated in some way. Many kinds of symmetry are recognised in science. But many processes are not symmetrical
Some chemical changes are said to be symmetrical because they are reversible. For example, the components of electrical batteries change when the battery is discharged but resume their previous condition when charged.
For time to be symmetrical, that is, if its direction could be “reversed”, all processes should be reversible in a similar way to these chemical interactions. That is, moving to the past is just the reverse of moving into the future. This idea can be depicted by playing a video backwards. The mathematics of relativity theory allows time to go “backwards” as well as “forwards”. But this doesn’t necessarily make it true. However, as will be mentioned later, the principle of quantum uncertainty may allow time to go backwards for very short moments.
The idea of time running backwards, while it may seem attractive, is generally regarded to be impossible. The parts of a shattered cup that has fallen onto a hard floor can’t be reassembled into an intact cup by a reverse action of the forces that caused the cup to break. No reversal of time will reassemble the shattered cup, or put the water back into it and make the cup jump back into your hand. So time is not symmetrical, and the second law of thermodynamics shows why it cannot be.
The Second Law of Thermodynamics
An example of the second law of thermodynamics is that if something hot (i.e., with a high temperature) is in close contact with something cooler, i.e., with a lower temperature, then heat will be transferred from the hot thing to the cooler thing, making them closer in temperature. But, unless there is outside interference, heat cannot be transferred from the cooler thing to the hotter one.
In essence, the second law of thermodynamics says that when there is a high energy potential associated with a low energy potential, some energy may transferred from the high to the low to reduce the difference between the potentials, but the transfer cannot go in the opposite direction to increase the difference. Temperature is the measure of heat potential. Similarly, pressure is a measure of mechanical potential. Voltage is electrical potential.
Another example of the second law of thermodynamics is colloquially illustrated in the saying that water always seeks its own level. It won’t spontaneously run uphill.
But, with any device or system that appears to defy the second law of thermodynamics, there is always some external energy source that makes the change in potential to apparently “go in the wrong direction”. The amount of energy needed for this is always greater than the amount of energy “saved” in cooling the refrigerator, or charging the battery or pumping the water uphill, etc. In every case, you have to put in electrical or some other kind of energy. So overall, differences of potential such as temperature are continually reducing throughout the universe and increasing its entropy.
This universal process of continual irreversible equalisation of potentials of any kind is the explanation of how time can have only one direction.
A Few More Concepts
A couple of other concepts relating to time will now need clarifying: what it means for something to be real, and what it means for something to exist. Being real may seem to be the same as existing, but I think there is a distinction between them.
There is a concept in science that being real means being consistent with the laws of physics. This doesn’t quite feel the same as the common concept of reality. But we do regard reality to be what we can detect with our senses and identify with our understanding.
We could regard the laws of physics (and the other sciences) to be the product of the most rigorous identification and understanding of everything that we have collectively detected. This does not mean that science or the laws of science are the absolute truth. I think they are the closest we have been able to get to the truth, but I have no idea how close that is.
I do not know of a better definition of reality, and I think it is a relevant concept for this discussion.
I think to exist means to be capable of having identifiable characteristics. Some people may disagree with this, and it raises the issue of how characteristics can be justifiably identified. Also, if a hypothetical entity can be given hypothetical characteristics, does it exist? Presumably it can if there is valid identification of the characteristics, but there would be argument about the validity of identification of any aspect of a hypothetical entity. In any case, I know of no better definition of the concept of existing.
Time, as part of space-time, is an entity that is intrinsic to the nature of the physical world and is an aspect of the laws of physics. So it is real. It is a component in the concepts of velocity, acceleration, force and energy. So it exists – except for those physicists who, as mentioned earlier, think it doesn’t.
But I think that time is not the same as the past plus the present plus the future. I think the past, present and future comprise all that happened, is happening and will happen. Time may be thought of as the path connecting them. But there is no definable path in the sense that could be described by, for example, being straight or crooked or by wide or narrow.
I can presume, but cannot be sure, whether the future will obey the laws of physics, but it is not obeying (or disobeying) them yet. However, I do think it can have characteristics. So if my definitions of being real and of existing are accepted, the future exists but is not yet real. Some philosophers think the future is real. I think that what is in the past was once real but I do not think it is still obeying the laws of physics. So once it becomes the past it is no longer real. I think the past has identifiable characteristics, so it exists. And I think the present exists and is real, however short its duration might be.
Another way to envisage time is to regard the universe to be like a machine that is operating in accordance with a set of rules. Time is the duration, from beginning to end, of each action within the universe. We measure the duration of incidents by making comparisons with devices, such as clocks, that have been shown to be consistent in their operations.
Two Pictures of the Universe
I will now give two depictions of the universe that represent two basic ideas about time. One is the Block universe, which gives equal status to past present and future. There are several versions of this .but I will present only one. The other is the Growing Block universe, which views the future as not yet existing. There are several versions of this also.
The Block Universe
The Block Universe represents the viewpoint known as Eternalism.
In this picture, every point in the four dimensional universe of space and time is precisely deterministic. The past, present and future are all equally real and all exist. Past and future are relative to some decision about where the present is regarded to be. The past and present are known and the future can be precisely predicted. The word now refers to our present location in time, and the word here refers to our present location in space. Travel to the past or future cannot occur. To get to the future you just have to wait until it becomes the present.
The different versions address problems about how we know we are in the present, how do we get from the present to the future, and the implications of the theory of relativity. Some “Eternalists” envisage being able to look down onto the whole of past present and future as a single entity.
The Block Universe usually implies the concept of continuity, which means that the universe is composed of infinitesimal (i.e., infinitely short) points of space and time, each point contacting seamlessly with those next to it.
But if the block universe were to be thought of as having quantum uncertainty, this would allow a very, very small scope for retrocausality, that is, the future occurring before the present – a sort of “time going backwards”. This, in turn, would help explain how the phenomenon of entanglement could occur. According to quantum mechanics, two particles can become “entangled”, which means that that if they then go apart on separate paths, measuring the particular conditions of one of them will immediately reveal the conditions of the other, no matter how far apart they are at the time. Without the concepts of a block universe and quantum uncertainty, entanglement would seem to imply that there could be communication between the particles at a speed exceeding the speed of light, which is forbidden by Einstein’s special theory of relativity.
The Growing Block Universe
This picture describes the universe as many scientists and philosophers and most of the rest of humanity would see it. It is structurally an extension of the Block Universe. The second law of thermodynamics applies, so motion through time must always progress, or grow, towards the future, and never go “backwards” towards the past, or stay still.
While the past and present can be precisely known and the future precisely predicted in the Block Universe, our knowledge is rather different in the Growing Block Universe. The “present time” is the three-dimensional “hyperspace” that is the growth face that continuously progresses towards the future. At this growth face, the probabilities of the future become actualities of the present. The “thinness” (or duration) of the present cannot be zero, because the quantity zero is too precise to be allowable by Heisenberg’s uncertainty principle, so the growth face does have some, miniscule, duration.
(Heisenberg’s uncertainty principle is one of the basic ideas of quantum theory. A rough description of it is that every aspect of the universe is very slightly “fuzzy”. In other words, there is no such thing as a completely exact size. This fuzziness is too small to have any significance for anything except the very tiniest parts of the universe. But the fuzziness means, among other things, that there cannot be anything that has a length that is exactly zero and there can be no duration of time that is exactly zero.)
So this growth face is three-dimensional space plus a very thin bit of time. You might imagine this thin slice of time happening uniformly across the entire universe, something like a flat plane surface. But you would be mistaken. In this universe, we cannot know what is happening precisely “now” in distant places because our observations depend on the finite speed of light. But we can know some time after it has happened. The amount of delay depends on how far away the particular event is from us. This is similar to watching a football being kicked some distance away and hearing the sound of the kick some short time after seeing it.
So the growth face should be more like a curved surface, with the “top” of the curve being at the location of each observer.
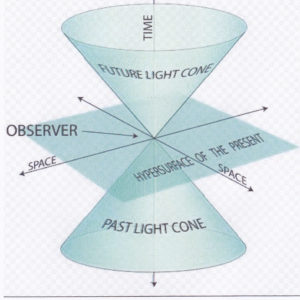
Also, the amount of delay in seeing what is “now” in distant places depends also on the distortions of space-time, in accordance with the theory of relativity. So the shape of the slice of the growth face is not smooth or a simple curve. It depends on the masses and speeds of all the objects between the viewers and the distant places. ( See the diagram below.) Also the appearance of the growth face would be different from each point of the universe.
So knowing precisely where something is “now” in outer space is a very complicated task. It makes you realise what an achievement it is to land a space ship on some distant planet or asteroid, when the space ship is moving at a speed of tens of km per hour, passing many massive objects on a journey of hundreds of millions of km that takes several years, and the destination is also moving very fast, and so is the earth. The Soviet Union was the first country to put a satellite into orbit around the earth because it had the best rockets. The USA was the first country to land a space ship on a distant object in space because it had the best computers.
The curved line represents how, when someone is looking at distant places, what is seen at those places “now” is what has already happened there. The more distant the observed place is, the further into the past is what the observer can see. The lower branch of the curve on the right hand side of the diagram illustrates how light passing through the gravitational field of some large object increases the delay in seeing what is happening at the distant places.
But it is not only “now” that is complicated. Each location in this universe has its own, restricted, past. For example, the only things in the universe that could have influenced us during the past five minutes must have been no further away from us than the distance that light can travel in five minutes. This is because, according to the special theory of relativity, nothing can travel faster than the speed of light.
It takes eight minutes for the light emitted by the sun to reach the surface of the earth. So an event on the sun that occurred five minutes ago could not have affected us during the past five minutes. But an event that occurred longer than eight minutes ago would have. Everything that could have affected us in the last five minutes of our past is everything within a sphere of space that is five light minutes (or about 90 million km) in radius with us at the centre.
Our past going back 5000 years would be a much larger sphere, with a radius of 5000 light years. But it would be completely different from that of some entity in a galaxy that was more than 5000 light years from us.
Similarly, every location in the universe has its own future. Scientists usually depict these concepts of past and future, in a way that represents the spheres of 3D space to as 2D circles. They then think of the past and future as “time cones”, with the points of the cones meeting at the present time and the circles as the opposite ends of the cones. This is shown in the diagram below
Light cones enclosing the volumes of the possible past and future of a particular location in the universe. Nowhere outside the cones could be the past or future of this location. Each point in the universe has its own light cones.
The sciences of cosmology, archaeology and biological evolution illustrate that the laws of physics apply to the past and the present. So in the growing block universe, there is evidence that the past and the present are real. Similarly, the characteristics of the past and present are identifiable, so they exist.
In this Growing Block universe, past and the present are real, and they exist. The future is probabilistically deterministic in accordance with quantum theory, so it is real. This doesn’t mean that we can make precise predictions the future, which we can’t. It means that what happens in the future is just the consequence of the laws of nature acting upon all of the conditions in the present. So we can often make good estimates, particularly of the near future
But the future is yet to be, so does it exist before it has occurred?
This Growing Block concept relies on a Copenhagen interpretation of quantum theory, (as distinct from the Many Worlds interpretations). So, if you accept this interpretation, you accept that you are living in the growing block universe.
For those who do not accept the Copenhagen interpretation, there is a Many Worlds interpretation. In this concept, there are many separate universes, each being the outcome of a different quantum probabilistic outcome for every event of every particle in each universe. In each universe there is only one way each quantum event can occur but the future is still probabilistic. This contrasts with Copenhagen view that a particle can be simultaneously in more than one condition until its wave function collapses and only one condition survives
In other respects each universe is like the Growing Block model. At present, we have no way of telling whether we are living in the Growing Block universe or in one – or very many – of the multiple universes. Of course, it could be none of the above.
With these and other pictures of the significance of time in the universe, the past, present and future are different and distinguishable from each other, irrespective of when and where the present is regarded to be. This would seem to demonstrate that all three exist. But the past, present and future do not constitute time. Time is what separates one period from another in the same way that space separates one location from another. (This is not what is implied in my poem at the beginning of this essay, but there is – or once was – the concept of poetic licence.)
SOME FURTHER ISSUES
Is Time Really a Dimension?
Although the theory of relativity regards time as the fourth dimension, time has differences from the dimensions of space. While space is a three-dimensional entity with two directions along each of its dimensions, time has only one dimension and one single direction. This single direction is recognised in most areas of physics. Despite the mathematics of the theory of relativity, there is no observed effect of time going backwards. And I do not think every solution to a mathematical representation of physics must have a physical consequence. (A simple illustration of this is the Pythagoras solution allowing a triangle to have one or two sides of negative length.)
The Heisenberg uncertainty principle may seem to allow time to sometimes go backwards, but no event that could defy the second law of thermodynamics can happen during that fleetingly uncertain period of time.
Also, energy is required to initiate a change in the position or velocity of an object in space, as described in Newton’s laws of motion. But the entire universe of space and matter seemingly progresses continuously along the direction of time with no apparent expenditure of energy or mass.
There is no concept of a growth face associated with movement through space that corresponds with the way the whole of space progresses through time.
Units of distance (i.e., the measurement of space) are not interchangeable with units of time in any of the dimensions of physical units. For example, time and distance are the dimensions of velocity (distance per time) and acceleration (distance per time squared). But it would be quite meaningless to use a unit of time as a substitute for a unit of distance in the measure of velocity or acceleration, or using a unit of distance as a substitute for a unit of time. And this applies to all concepts that include an element of time.
There are no problems with the idea of reversing direction in any dimension of space. Strangely, perhaps, while any of the three dimensions of space by itself is symmetrical, reversing all three directions of space together turns out to be not symmetrical. Another aspect of something that is not symmetrical is electrical charge. That is, if everything with a positive electrical charge actually had a negative charge while everything with a negative charge actually had a positive charge, the condition of the universe would become significantly different. These things have been demonstrated to be true by theory and by experimental evidence of the behaviours of particles. But, at least theoretically, if time, space and electrical charge were all “flipped” together, the whole situation would still behave in the same way as before the flip. Does this mean that time is reversible after all? I think the answer is possibly, but not in this world.
(In his book A Brief History of Time, Stephen Hawking refers to “imaginary time”. This does not imply that time has an imaginary direction in addition to the direction we are familiar with. When scientists were first doing calculations relating to the theory of relativity they found some of the equations could be solved if they used complex numbers, which have imaginary components. But there is no such physical entity as imaginary time.)
What does all this say about time being a dimension? Time is obviously closely associated with the dimensions of space, but it is clearly not a dimension of space. Time is eminently measurable. Mass, length and electric charge are also measurable, and all, plus time, are classified together as the physical dimensions. Each is uniquely different from all of the others. Together, they are all essential; together they seem to be sufficient. So, despite opinions to the contrary, time is real, it exists and is a dimension.
Does Time Flow?
The concept of time “flowing” is understandable but it is not a good description. While observation, and the second law of thermodynamics, confirm what we may think of as the progress of time, the term flowing can have connotations of a river or a wind, which is very different from the concept of time. This would imply a speed of flowing, but what would be the units of its speed? Would they be seconds per second? (This would have no relationship to the concept of acceleration, which is defined as distance per second per second.)
It is not time that “progresses”: it is that space either “progresses”, or grows – apparently spontaneously – in one direction along the dimension of time. Perhaps time is like the course of the river and the past present and future are like the water and everything in and on it. The future, presumably, would be upstream, and the past, perhaps, when the river flows into the sea. But this doesn’t feel like a good metaphor. Where, for example, is the present time in this body of flowing water?
Some philosophers and scientists will object to the concept of time flowing as implying some guiding principle, or, like space, having more than one dimension.
How fast is the “passage” of time?
Subjectively, we think time sometimes passes very quickly and sometimes we think it goes slowly. There are two old sayings about this: time flies, and time plods on with leaden feet.
As discussed earlier, we have time “lengthening”, i.e., “going more slowly”, by various amounts, as the effects of speed and gravitational force. So if time has different lengths, the question is sometimes asked, ‘What is the standard by which time is measured’. Some people think that this question implies another kind of time to measure “ordinary” time by, a hidden time that we cannot identify. From this it is sometimes concluded that there is no such thing as time.
The theory of relativity refers also to the lengthening of distance, i.e., of space, as a consequence of speed and gravity. So similar questions to those asked about time might be asked about space. The most common way of measuring distance is to use some physical object marked with gradations of length. But in the International System of Units, which is the official standard used for measurements in physics, length is defined as the amount of time light takes to travel the distance being measured.
In other words, to measure length we use some calibrated physical object, such as a measuring tape or a clock. And to measure time we use some kind of clock. Both kinds of measuring instrument are calibrated using arbitrary units, such as metres and seconds, or multiples and submultiples: e.g., kilometres/nanometres and years/nanoseconds.
When the measuring processes are accurate enough, it is possible to measure particular phenomena and see how long they take under different degrees of speeds or gravity. Earlier, when discussing the theory of general relativity, I gave an example of a clock at ground level running more slowly than an identical clock on a geostationary satellite. The lengthening of time on the clock at ground level compared with the clock on the satellite might be expressed in, for example, nanoseconds per hour.
And more generally, at a certain relative speed or for a certain difference of the strength of the gravitational field, the lengthening is a certain percentage of the “normal” measure of time or space.
“Normally” time “passes” at the rate of one second per second, and space extends at the rate of one metre per metre.
Beginning and end of time
There is another kind of issue: was there a beginning of time? Some physicists say that time began with the big bang. Was there a universe, and time, before the big bang? If so did time occur before or after there was a universe? How could there have been such a thing as a time before the beginning of time? Could there have been such a thing as a universe before the beginning of time? How could time, or anything else in the universe, begin in a universe in which there was no such thing as time? These are paradoxes. We might to resolve them by saying that time and the universe are both infinite. If time were infinite, everything that could possibly have happened would have happened already, and there would be nothing new to happen. There seems to be no similar kind of paradox relating to space.
Could time have an ending? Would that be a time when nothing whatever happened? Perhaps that might occur if the universe reached a condition of absolute absence of difference in energy potential, such as a completely uniform temperature. Quantum theory disallows the possibility of absolute precision in any characteristic, so, if quantum theory is absolutely correct, time could not end. If time has no ending, i.e., an infinite future, does it also have an infinite past? If it had an infinite past, then, according to the second law of thermodynamics the universe would have been reducing its differences in temperature etc., for an infinite amount of time, and would have already reached its endless quantum stagnation. This is not, of course, our present situation.
Could space have an ending? Some scientists think the universe is infinite in size, so it would have no ending. This would imply that space must have been infinite at the big bang, which I think no physicist would accept – unless they thought, as some do, that the big bang was just an incident in something much bigger than “our” universe.
Other scientists think that, spatially, the universe is finite but unbounded. They liken it to the surface of a sphere, which is limited in size, but there could be movements around the surface that would eventually cross their own previous paths or come to their starting points. There would be nothing “outside” this curved surface. But there seems to be no equivalent concept of time being finite but unbounded in the way that space could be. However, it is the fact that space has more than one dimension that allows it to be finite but unbounded. And it could have other shapes than spherical.
All of these things show that there are fundamental differences between time and space, and that they must have aspects that we know nothing about.
All of what I have said is conditional on whether our present concepts of physics truly represent the nature of the universe. It may be that we can say no more than that the whole of physics, including time, is just how things appear from our limited point of view.
But what about a more popular perplexing issue; time travel?
Time Machines and Time Travel
The idea of travelling to specific times in the past or the future is very attractive. It was popularised in the novel The Time Machine by H. G. Wells, which was published in 1895, in which a man travels in a machine he has made to the year 802, 701, and spends an adventurous week there. He then returns and tells his friends about his past week in the future. It is an interesting story, and it raises several considerations.
When we travel from place to place, that is, moving through space, time is also elapsing. So in a sense we are also travelling through time. So would travelling in a time machine involve travelling also through space? If so, that could mean deciding where to arrive as well as when. Would we have to take account of the motion of the earth about the sun, and the motion of the solar system and of the galaxy?
When we travel to a distant place we pass through intermediate places. So would travelling in a time machine involve travelling through all the intermediate times, perhaps like the fast-forward or the rewind of an audio or video tape? If so, how fast would the journey be, and would there be the experience of fleeting sights and sounds during the journey? Or would it be like travelling in an aircraft, and/or being unable to see outside?
How possible would it be for someone to travel to some future time before it has actually occurred, or to some period in the past? Does the second law of thermodynamics, which relates to the use and consumption of energy and an increase in entropy, have anything to say about this?
Travelling to the future in a time machine would presumably involve the consumption of energy and would contribute, in advance, to the increase in entropy of all periods of time between the departure and arrival. This would not seem to violate the second law of thermodynamics. But the return journey might. It would be equivalent to moving to the past.
Presumably, moving to the past in a machine would require the consumption of energy. That would increase the entropy at the time of the destination, and at all subsequent periods of time. So the journey would have needed to consume no energy or a negative amount. Could “running backwards in time” generate energy in a way analogous to a trolley running down a hill? No, even this results in an increase in entropy.
It is hard to see how a time machine with someone in it could operate without energy. So travelling to the past would seem to violate the second law, since every physical process consumes energy.
(Does our progress through time in the “normal” way, consume energy? It is hard to see how we could know: If it does, we are unaware of the nature of any underlying process that might cause it. I do not think we could regard the progress through time as an event comparable with the actual events that are occurring and increasing entropy. It may be that there are two kinds of dark energy, one causing the expansion space and the other causing the expansion of time. But I am unable to see how this issue might be resolved.)
There are other fanciful conjectures based on the idea of time travel, such as travelling to the time and place of a grandparent’s childhood and killing the grandparent. This would mean that you cannot therefore exist. This is sometimes proposed as a proof of the impossibility of time travel.
This idea contains a common assumption: that when you in your time machine at some other period of time, you are still your present-day self, not the “you” at the time and place of arrival, and you can do things when you get there.
When you travel in a “space machine” (i.e., the car or train or whatever you travelled in) and arrive in another place, your age and the conditions of everything at your destination are those of your time of arrival at that place. In the same way, if it were possible for someone to “travel” to some particular time in the past, everything and everyone there would be exactly the way they were at that time at that place.
If you were to travel to a time ten years in the past, then when you arrived you would be exactly where you were ten years ago, and you would be ten years younger than your present age. If you were not part of a specific period in the past, say 100 years ago, then you could not be there when the time machine arrived. And if your particular time machine did not exist then, it could not get there either.
If there had been a time machine at the time your grandfather was alive, you could not be able to get out of the machine when you returned to kill your grandfather, unless you had, at that time, come out of the same machine previously. If you did get out, everything that happened from then would be an exact repetition of your life since then. So that’s one death that Grandfathers don’t need to worry about.
And if the machine travelled to some future time, you might be in a grave in some cemetery, but not in the time machine when it arrived.
If you were to travel into a future time and arrive alive and then come back, you would not remember anything about what happened in that future time once you got out of your time machine when you returned. (if you could get out) And then, if you ever got to that future period again by the normal passage of time, you would get into the time machine, which would be there, and go back. You would do this forever. So if you want eternal life, build a time machine – but don’t travel too far into the future.
Also, you could never go back to a previous time and get out of your time machine unless you had previously gone there in a time machine and got out, which, of course, you could not have done. So all juvenile potential grandfathers are safe from murderous grandchildren.
Of course, everything that I have just said could not happen might be possible in some other universe.
But, even in our universe, there could be time travel of a different kind. Theoretically, “wormholes in space-time” could provide shortcuts to remote parts of the universe and to other periods of time. There are suggested conditions by which wormholes might occur. One suggested wormhole would connect two black holes. But the journeys to the opening at one end and then out from the exit at the other end would each destroy a human body.
But, even if wormholes could feasibly be shortcuts to distant regions of space and time, would they act like the imagined time machines, and would they be subject to the same constraints and paradoxes as with time machines?
That will have to wait for a different time.
-0-
Referring to the article Finding the Flow (21 April2018, p29), the cover of New Scientist says, “You’re living in a moment that science says does not exist”, which seems to imply that time does not exist. In the text of the article there is a caption “We might soon be able to see time passing at two speeds at once”, which seems like “science” affirming that time does exist.
On the issue of whether time passes, there is a quotation “In a universe with every possible state coexisting, there is no passing time”, which would be true if superposition never collapsed and nothing ever happened.
The discussion of times’ arrow seems to be looking at surface issues rather than fundamentals. It suggests that the second law of thermodynamics is based on the probability of events happening, and the “law of averages”. It questions whether we are able to know if the same law of averages applies throughout the universe., and then uses this to cast doubt on the universality of the second law of dynamics as the arrow of time. I think these probabilities, whether expressed in terms of the behaviour of particles or in the concept of entropy, are merely outcomes of the second law of thermodynamics. The second law is the description of the interaction of forces that have their own ways of operating and are subject to the effects of relativity and quantum theory, as described by vector and tensor analysis. Moreover, the dimensions of all forces rely on mass, distance and time.
Two aspects of the fundamental forces are that they arise from the action of certain fundamental particles, and they progressively separated out from the universal force just after the big bang. All these processes involve a “before” and an “after” which requires the existence of time. Every change in the condition of everything in the universe has a “before” and an “after”. This is blurred at times by the outcomes of relativistic and quantum interactions that illustrate some of the characteristics of time, but the second law is the underlying principle.
As to what time is, we can describe it only in terms of observations of the world around us, in conjunction with concepts relying also on mass and distance. In the same way, we can describe mass and distance only in terms of observations of the world around us, in conjunction with the other concepts.